Contents

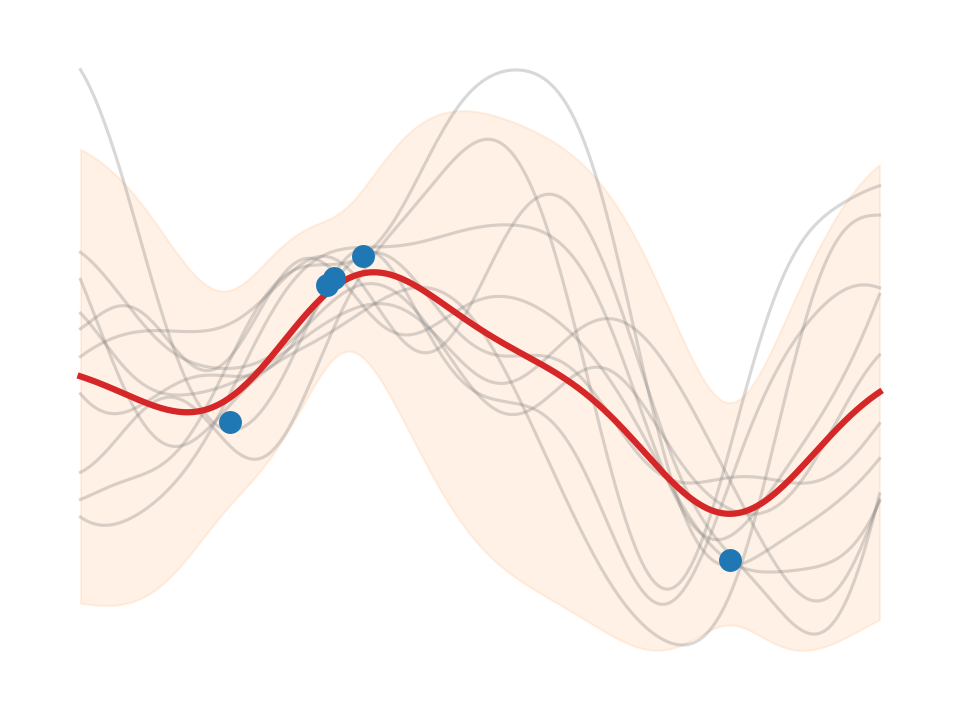
About

This project explores selected aspects of Gaussian processes (GPs) by implementing them (a.k.a. “learning by hacking”).[1]

Content

GP intro

Unless stated otherwise, we use the Gaussian radial basis function (a.k.a. squared exponential) as covariance (“kernel”) function

κ(xi,xj)=exp⁡(−‖xi−xj‖222ℓ2)

Notation:

  • RBF kernel length scale parameter: ℓ = length_scale (as in sklearn)

  • likelihood variance σn2 (a.k.a. “noise level”) in GPs, regularization parameter λ in KRR: η = noise_level (as in sklearn)

  • posterior predictive variance: σ2

Resources

[Bis06]

Christopher Bishop. Pattern Recognition and Machine Learning. Springer, 2006. URL: https://www.microsoft.com/en-us/research/publication/pattern-recognition-machine-learning/.

[DLvdW20]

Marc Peter Deisenroth, Yicheng Luo, and Mark van der Wilk. A practical guide to gaussian processes. 2020. URL: https://infallible-thompson-49de36.netlify.app/ (visited on 2020-12-03).

[GKD19]

Jochen Görtler, Rebecca Kehlbeck, and Oliver Deussen. A Visual Exploration of Gaussian Processes. 2019. URL: https://distill.pub/2019/visual-exploration-gaussian-processes (visited on 2022-11-22), doi:10.23915/distill.00017.

[KHSS18]

Motonobu Kanagawa, Philipp Hennig, Dino Sejdinovic, and Bharath K. Sriperumbudur. Gaussian Processes and Kernel Methods: A Review on Connections and Equivalences. 2018. URL: http://arxiv.org/abs/1807.02582, arXiv:1807.02582.

[Mur23]

Kevin P. Murphy. Probabilistic Machine Learning: Advanced Topics. MIT Press, 2023. URL: https://probml.github.io/pml-book/book2.html.

[RW06]

Carl Edward Rasmussen and Christopher K. I. Williams. Gaussian Processes for Machine Learning. MIT Press, 2006. ISBN ISBN-10 0-262-18253-X. URL: http://www.gaussianprocess.org/gpml.

Citing

The source code and this book are licensed under the BSD 3-Clause License. If you re-use material from this work or just like to cite it, then either use this BibTeX entry

@Online{schmerler_GPPlayground,
  author   = {Steve Schmerler},
  title    = {GP Playground},
  url      = {https://github.com/elcorto/gp_playground},
  subtitle = {Explore selected topics related to Gaussian processes},
  doi      = {10.5281/zenodo.7439202},
}

or the DOI 10.5281/zenodo.7439202.

Contents