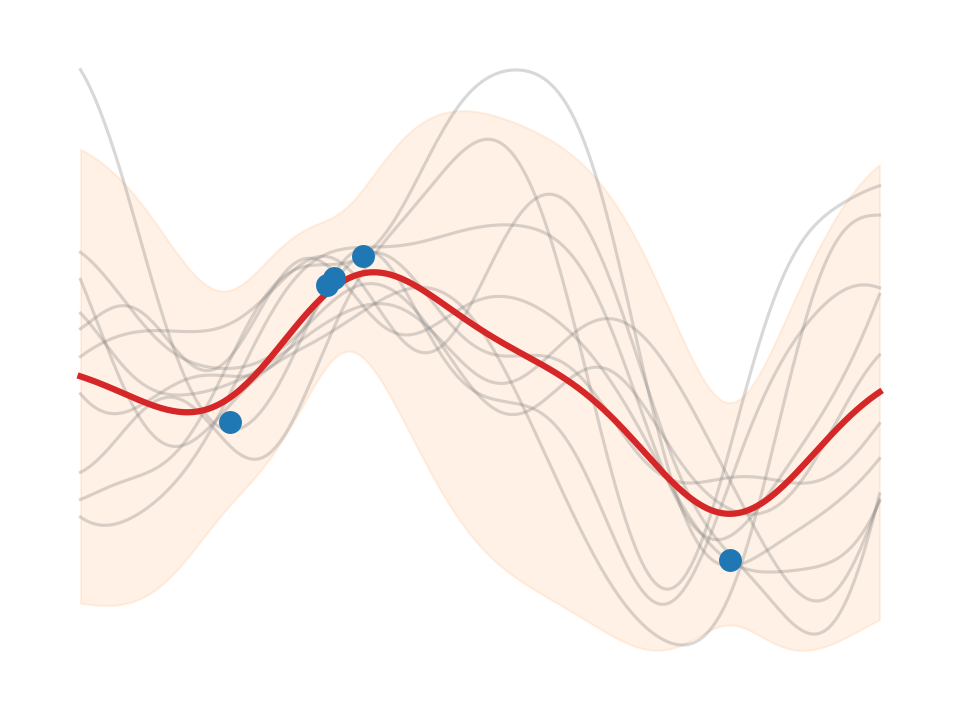
Reference implementation of RW06 equations

Here we implement simple but instructive reference code in numpy by direct translation of the core equations of [RW06].

from functools import partial

from scipy.spatial.distance import cdist
from scipy import linalg
import numpy as np


def rbf_gauss(rsq, length_scale):
    return np.exp(-0.5 * rsq / length_scale**2.0)


def kernel(X1, X2, **kwds):
    return rbf_gauss(cdist(X1, X2, metric="sqeuclidean"), **kwds)


def sym_solve(A, b):
    return linalg.solve(A, b, assume_a="sym")


def cov2std(y_cov):
    return np.sqrt(np.diag(y_cov))


def sample_y(y_mean, y_cov, n_samples=1, random_state=123):
    """What GaussianProcessRegressor.sample_y() does, but since sklearn can't
    do predict_noiseless() and generate noiseless samples when WhiteKernel is
    used, it is easier to have custom sample_y code.

    Re-implements core part of sklearn's sample_y(). Note that sklearn (v1.1.2)
    still uses np.random.RandomState (other default RNG), so even with the same
    seed, we get different samples.
    """
    rng = np.random.default_rng(seed=random_state)
    return rng.multivariate_normal(y_mean, y_cov, n_samples).T


def textbook_prior(noise_level=0, **kernel_kwds):
    """
    R&W 2006, eq. 2.17 (if noise_level=0)
        X*        = X_pred  = X'
        K(X*, X*) = K_pp    = K''
    """
    kern = partial(kernel, **kernel_kwds)

    def predict(X_pred):
        K_pp = kern(X_pred, X_pred)
        K_pp_noise = K_pp + np.eye(X_pred.shape[0]) * noise_level
        y_mean = np.zeros((X_pred.shape[0],))
        y_cov = K_pp_noise
        y_std = cov2std(y_cov)
        return y_mean, y_std, y_cov

    return predict


def textbook_posterior(X_train, y_train, *, noise_level=0, **kernel_kwds):
    """
    R&W 2006, eqs. 2.23, 2.24
        X         = X_train
        X*        = X_pred  = X'
        K(X, X)   = K_tt    = K
        K(X*, X)  = K_pt    = K'
        K(X*, X*) = K_pp    = K''
    """

    kern = partial(kernel, **kernel_kwds)
    K_tt = kern(X_train, X_train)
    K_tt_noise = K_tt + np.eye(X_train.shape[0]) * noise_level
    alpha = sym_solve(K_tt_noise, y_train)

    def predict(X_pred):
        K_pt = kern(X_pred, X_train)
        K_pp = kern(X_pred, X_pred)
        y_mean = K_pt @ alpha
        ##y_cov = K_pp - K_pt @ linalg.inv(K_tt_noise) @ K_pt.T
        y_cov = K_pp - K_pt @ sym_solve(K_tt_noise, K_pt.T)
        y_std = cov2std(y_cov)
        return y_mean, y_std, y_cov

    return predict


def textbook_posterior_noise(*args, **kwds):
    """
    Same as textbook_posterior, only that

        y_cov += np.eye(X_pred.shape[0]) * noise_level
    """

    def predict(X_pred):
        y_mean, _, cov = textbook_posterior(*args, **kwds)(X_pred)
        y_cov = cov + np.eye(X_pred.shape[0]) * kwds["noise_level"]
        y_std = cov2std(y_cov)
        return y_mean, y_std, y_cov

    return predict